Kinetic Molecular Theory Illustrated with LAMMPS

Introduction

The Kinetic Molecular Theory (KMT) explains the motion of gas particles and how this motion relates to macroscopic properties like temperature and pressure. To illustrate KMT, we simulate an ideal gas inside a cubic box using LAMMPS. The simulation tracks particle positions and velocities under perfectly elastic reflections at the walls, allowing us to visualize particle motion and compute kinetic energies.

Simulation Setup

The simulation uses a cubic box of size 100 × 100 × 100 with 100 argon-like particles. Periodic boundary conditions are replaced by fixed reflecting walls in all directions. Particles are initially assigned velocities corresponding to 300 K using a random seed. We evolve the system with the NVE ensemble (constant number of particles, volume, and energy).

Visualization

The trajectory from the LAMMPS dump file can be converted using OVITO into a GIF to illustrate particle motion over time. Below is an example of how the particles move inside the box, reflecting off the walls elastically.

Particle motion in simulation box

Kinetic Energy: Theory vs Simulation

According to KMT, the theoretical kinetic energy per particle in 3D is

\[ KE_\text{theoretical} = \frac{3}{2} k_B T \]

Here, \(k_B\) is the Boltzmann constant, \(T\) is the absolute temperature, and \(N\) denotes the total number of molecules in the system. The total kinetic energy of the gas is

\[ KE_\text{total,theory} = \frac{3}{2} N k_B T \]

Using \(k_B = 8.617\times10^{-5}\,\text{eV/K}\), \(N = 100\), and \(T = 300\,\text{K}\), we find:

\[ KE_\text{total,theory} = \frac{3}{2} \cdot 100 \cdot (8.617\times10^{-5}\,\text{eV/K}) \cdot 300\,\text{K} \approx 3.88\,\text{eV} \]

The simulated kinetic energy is computed using the particle velocities extracted from the LAMMPS dump file. For each particle, we calculate \[ v = \sqrt{v_x^2 + v_y^2 + v_z^2} \] and sum over all particles where i is placeholder for atom index at any timestep: \[ KE_\text{sim} = \frac{1}{2} m \sum_i (v_{x,i}^2 + v_{y,i}^2 + v_{z,i}^2) \]

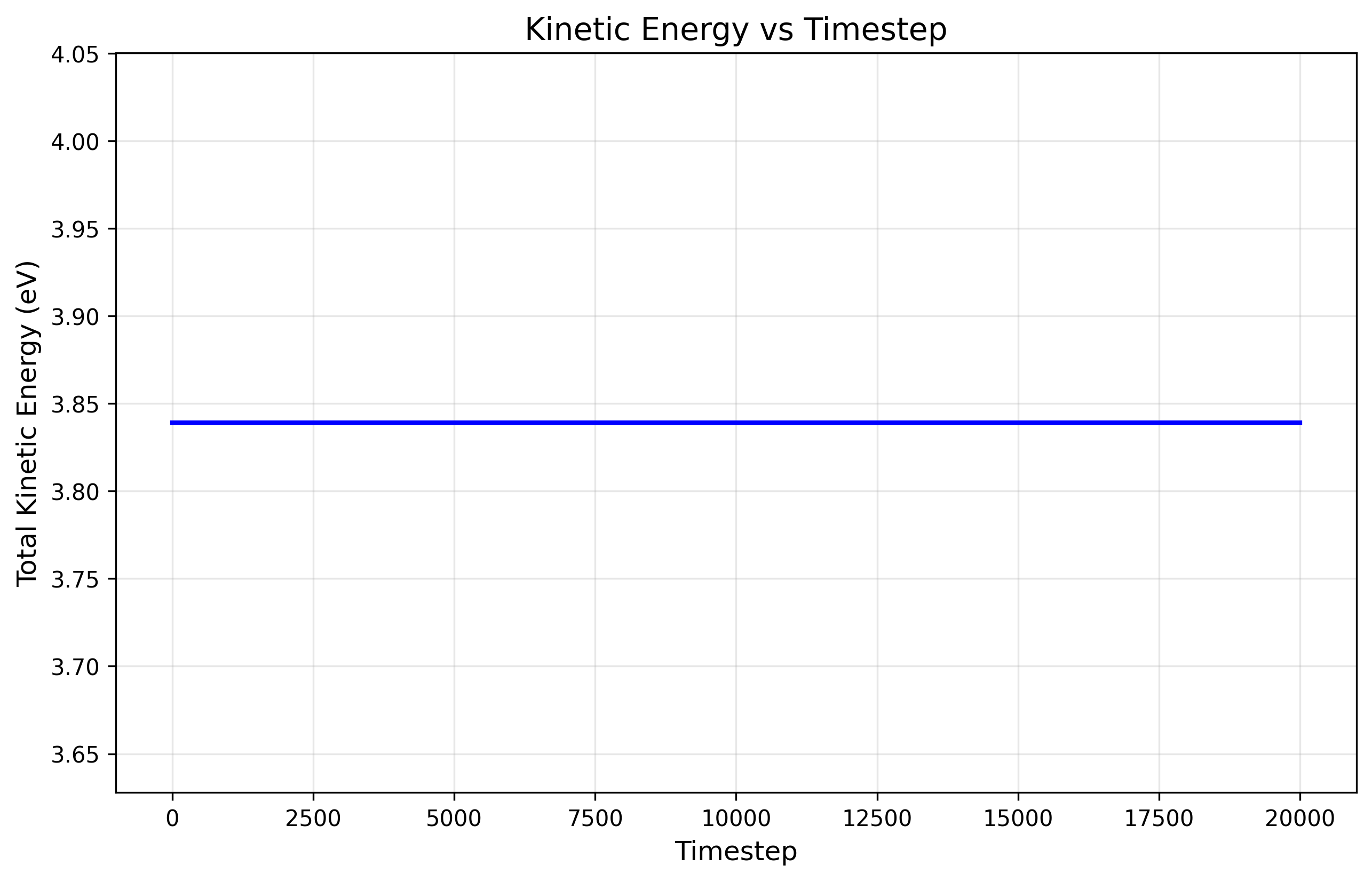
Particle motion in simulation box

For this simulation, the kinetic energy we found is 3.83 eV. Since this is an ideal gas with no intermolecular attractions, the total energy of the system is just the kinetic energy.

Conclusion

This simulation demonstrates the core ideas of the Kinetic Molecular Theory (KMT):

• Particles move in constant velocity in a straight line.

• Particles collide elastically with the walls of the simulation box.

• Kinetic energies of particles are consistent with the system temperature.

So, using LAMMPS and Python, we can visualize particle motion, compute kinetic energies, and compare simulation results with theoretical predictions.

All the code for this simulation is available at GitHub.